knapsack

背包神奇小 trick 学习笔记

碎碎念

先占个坑，明天写。

本文基本都是复读某个 CF博客（可能会附带例题）

CF博客链接：here

Part1：背包的基本问题定义

01-背包

有 $n$ 个物品，第 $i$ 个重量是 $w_i$，价值是 $v_i$，找到一个集合 $S$，使得 $\sum\limits_{i\in S}w_i\leq C$，并且使得 $\sum\limits_{i\in S}v_i$ 最大化。

多重背包

有 $n$ 个物品，第 $i$ 种有 $a_i$ 个，重量是 $w_i$，价值是 $v_i$，找到一组序列 $t$，使得$\forall i\in[1,n]$ 有 $t_i\leq a_i$， $\sum\limits_{i\in S}w_it_i\leq C$， $\sum\limits_{i\in S}v_it_i$ 最大化。

子集和

有 $n$ 个物品，第 $i$ 个重量是 $w_i$，找到一个集合 $S$，使得 $\sum\limits_{i\in S}w_i=C$。

在阅读本文前，请确保您已经会在 $O(nC)$ 的复杂度解决第一个，在 $O(nC\sum a)$ 的复杂度解决第二个，在 $O(\frac {nC} \omega)$ 的复杂度解决第三个。

Part2：子集和的优化

优化1：二进制分组

有 $n$ 个物品，第 $i$ 个重量为 $w_i$，定义 $\sum\limits_{i=1}^n w_i=C$，对于每个 $k\in [1,C]$，判断是否存在集合 $S$，使得 $\sum\limits_{i\in S}w_i=C$。

我们可以在 $O(\frac {C\sqrt C} \omega)$ 的复杂度内解决这个问题。

首先我们来考虑一个看上去是 $O(\frac {C\sqrt C\log C} \omega)$ 的算法。

把 $w_i$ 相同的合并，然后会变成 $m$ 组，第 $i$ 组有 $a_i$ 个重量为 $w_i$ 的物品。

容易发现，由于不同组的 $w_i$ 不同，所以 $m$ 是 $O(\sqrt C)$ 级别的。

然后对 $a_i$ 进行二进制分组，具体来说就是把这一组分成 $w_i,2w_i,4w_i,...$，每次把 $a_i$ 减掉一个 $2$ 的次方，最后剩下一个不是 $2$ 的次方的数单独放，每个看作一个独立的物品做 0-1背包。可以证明这样一定能表示出来 $1$ 到 $a_i$ 之间的任意数个 $w_i$，比如 $20w_i$ 分解为 $w_i,2w_i,4w_i,8w_i,5w_i$，$35w_i$ 分解为 $w_i,2w_i,4w_i,8w_i,16w_i,4w_i$。

这个做法明显有一个很松的上界是 $O(\frac {C\sqrt C\log C}\omega)$。

实际上是 $O(\frac {C\sqrt C} \omega)$ 的。

考虑能贡献出 $k·w_i$ 的组合，记为 $S_k$，于是我们想要证明 $\sum_{k\geq1}|S_k|=O(\sqrt C)$。

首先，我们能注意到大多数新重量为原来已有的重量的 $2^k$ 倍。对于每个组，只会贡献最多一个不是 $2$ 的次幂的新重量。所以，如果我们能证明 $\sum\limits_{k=2^z}|S_k|=O(f(C))$，那么我们就能证明出 $\sum_{k>=1}|S_k|=O(f(C)+\sqrt C)$。

显然 $\sum\limits_{i\in S_k}w_i\leq \frac C k$，所以得出结论 $|S_k|\leq \sqrt {\frac C k}$。

所以，$\sum\limits_{k=2^z} |S_k| \leq \sum\limits_{z \geq 1} \sqrt \frac{C}{2^z} = \sqrt C \left (\sum\limits_{z \geq 1} \frac{1}{\sqrt {2^z}} \right) = O(\sqrt C)$。

另一个更简洁的证明：

考虑从小到大处理重量，用一个初始为空的表 $W'$ 作为我们的新重量。假设有 $occ$ 次最小的 $w$ 出现。如果 $occ$ 是奇数，我们添加 $\frac {occ-1} 2$ 次 $2w$ ，$1$ 次 $w$ 进 $W'$。如果 $occ$ 是偶数，我们添加 $\frac {occ-2} 2$ 次 $2w$ ，$2$ 次 $w$ 进 $W'$。

不难发现 $|W'|\leq 2\sqrt C=O(\sqrt C)$ 因为我们每个重量最多只往 $W'$ 中加了 $2$ 次。

例题：CF755F

最大值很好做，就是直接贪心。最小值就是判断子集和，为上述板子，贴个代码。

#include<bits/stdc++.h>
#define forn(i,a,b)for(int i=(a),_b=(b);i<=_b;i++)
#define fore(i,b,a)for(int i=(b),_a=(a);i>=_a;i--)
#define rep(i,n)for(int i=0,_n=n;i<n;i++)
#define ll long long
#define pii pair<int,int>
#define m_p make_pair
#define pb push_back
#define fi first
#define se second
#define int ll
#define foreach(i,c) for(__typeof(c.begin())i=(c.begin());i!=(c).end();i++)
using namespace std;
const int N=1000010;
int n,m,k;
int a[N],b[N],c[N];
bitset<N>dp;
bool vis[N];
int cnt1=0,cnt2=0;
int dfs(int x){
	if(vis[x])return 0;
	vis[x]=1;
	return 1+dfs(a[x]);
}
int t[N];
signed main(){
    cin.tie(0);cout.tie(0);
	ios::sync_with_stdio(0);
	cin>>n>>k;
	forn(i,1,n)cin>>a[i];
	forn(i,1,n){
		if(vis[i])continue;
		b[++m]=dfs(i);
	}
	forn(i,1,m){
		c[b[i]]++;
		cnt1+=b[i]/2;
		cnt2+=b[i]%2;
	}
	dp.reset();dp.set(0);
	forn(i,1,n){
		int x=1;
		while(x<=c[i]){
			dp|=dp<<(x*i);c[i]-=x;x*=2;
		}
		if(c[i]){
			dp|=dp<<(c[i]*i);
		}
	}
	int ans1=k,ans2=0;
	if(!dp[k])ans1++;
	forn(i,1,k){
		if(cnt1){
			ans2+=2;
			cnt1--;
		}
		else if(cnt2){
			ans2++;
			cnt2--;
		}
	}
	cout<<ans1<<" "<<ans2<<"\n";
	return 0;
}

优化2：状态设计剪枝

有 $n$ 个物品，第 $i$ 个重量为 $w_i$，满足 $\forall i\in[1,n]$，$w_i\leq D$。找到一个集合 $S$，使得 $\sum\limits_{i\in S}w_i=C$。

这个问题可以在 $O(nD)$ 的复杂度解决。

首先 $O(n^2D)$ 的瓶颈在于，选一个不超过 $D$，但是 dp 状态要维护 $O(nD)$ 个。

于是我们考虑舍弃一些，大致思路为，找到最大的 $k$，满足 $\sum\limits_{i=1}^k<C$，如果 $k=n$，肯定不行，直接不考虑。

然后我们先把 $1$ 到 $k$ 全选，在后面的过程中从后面选一些，从前 $k$ 个扔掉一些，如果能找到合适的顺序满足重量和始终在 $[C-D,C+D]$ 这样一个 $O(D)$ 的范围内波动，那我们就成功了。

记 ${\rm can}(sum,l,r)$ 为状态，这个值为真当且仅当能满足 $\sum\limits_{i=1}^{l-1}w_i+\sum\limits_{i=l}^r w_it_i=C$，$t_i\in \{0,1\}$。

发现固定住 $sum$ 和 $r$ 的时候这个状态关于 $l$ 是有单调性的，于是我们把 $l$ 设进状态就可以省去一维了。

${\rm dp}(sum,r)$ 为最大的 $l$ 满足 ${\rm can}(sum,l,r)$ 为真。

容易发现这个 ${\rm dp}$ 在 $sum$ 固定时关于 $r$ 也是有单调性的，具体地，${\rm dp}(sum,r-1)\leq {\rm dp}(sum,r)$。

考虑转移，下面的所有转移都是取 $\max$ 操作。

第一种，拓展 $r$，有 ${\rm dp}(sum,r-1)\rightarrow {\rm dp}(sum,r)$ 和 ${\rm dp}(sum,r-1)\rightarrow {\rm dp}(sum+w_r,r)$，分别是不选和选 $w_r$。

第二种，拓展 $l$，对于一个状态 ${\rm dp}(sum,r)=l$，我们找所有的 $l'<l$ 进行转移，${\rm dp}(sum-w_{l'},r)\leftarrow l'$。

但第二种转移是 $O(n)$ 的，这很不好。

稍微想想后发现，对于 $l'<{\rm dp}(sum,r-1)$ 已经在上一轮被更新过了，所以我们只需要更新 $sum$ 上一轮的 ${\rm dp}$ 值到这一轮的之间的 $l'$，具体地，${\rm dp}(sum,r-1)\leq l'<{\rm dp}(sum,r)$。

这样下来对于每一个 $sum$ 更新的 $l'$ 总和是 $O(n)$ 的$，sum$ 固定在 $O(D)$ 的范围内，故总和是 $O(nD)$ 的。

例题：ABC221G

先把曼哈顿距离转成切比雪夫距离，这样横纵坐标互不影响，然后就是这个问题的板子。贴个代码。

#include<bits/stdc++.h>
#define forn(i,a,b)for(int i=(a),_b=(b);i<=_b;i++)
#define fore(i,b,a)for(int i=(b),_a=(a);i>=_a;i--)
#define rep(i,n)for(int i=0,_n=n;i<n;i++)
#define ll long long
#define pii pair<int,int>
#define m_p make_pair
#define pb push_back
#define fi first
#define se second
#define int ll
#define foreach(i,c) for(__typeof(c.begin())i=(c.begin());i!=(c).end();i++)
using namespace std;
const int N=2010,D=1800;
int n,A,B;
int S=0;
int d[N];
int dp[D*2+10][N]; 
pii frm[D*2+10][N]; 
bool t[2][N];
bool flag=1;
void upd(int &x,int y){
	if(y>x)x=y;
}
void solve(int C,int z){
	int sum=0;
	int k;
	forn(i,1,n){
		sum+=d[i];
		if(sum>=C){
			k=i;break;
		}
	}	
	if(sum<C){
		flag=0;return;
	}
	sum-=d[k];
	memset(dp,0,sizeof(dp));
	dp[sum-C+D][k-1]=k;
	forn(i,k,n){
		forn(s,-D,D){
			upd(dp[s+D][i],dp[s+D][i-1]);
			if(s+D+d[i]<=D+D)upd(dp[s+D+d[i]][i],dp[s+D][i-1]);
		}
		fore(s,D,-D){
			forn(j,dp[s+D][i-1],dp[s+D][i]-1){
				if(s+D-d[j]>=0)upd(dp[s+D-d[j]][i],j);
			}
		}
	} 
	if(!dp[D][n])flag=0;
	else{
		int p;
		sum=D;p=n;
		forn(i,1,k-1)t[z][i]=1;
		while(p!=k-1){
			bool ok=0;
			int j=dp[sum][p];
			if(sum+d[j]<=D+D&&j>=dp[sum+d[j]][p-1]&&j<dp[sum+d[j]][p]){
				ok=1;sum=sum+d[j];t[z][j]^=1;
			}
			if(ok)continue;
			if(dp[sum][p-1]==dp[sum][p]){
				p=p-1; 
				continue;
			}
			if(sum-d[p]>=0&&dp[sum-d[p]][p-1]==dp[sum][p]){
				sum=sum-d[p];t[z][p]^=1;p=p-1;
				continue;
			}
		}
	}
}
void print(){
	if(!flag){
		cout<<"No\n";return;
	}
	cout<<"Yes\n";
	forn(i,1,n){
		if(t[0][i]&&t[1][i])cout<<"R";
		if(t[0][i]&&!t[1][i])cout<<"U";
		if(!t[0][i]&&t[1][i])cout<<"D";
		if(!t[0][i]&&!t[1][i])cout<<"L";
	}
}
signed main(){
    cin.tie(0);cout.tie(0);
	ios::sync_with_stdio(0);
	cin>>n>>A>>B;
	forn(i,1,n)cin>>d[i],S+=d[i];
	int tmp1=A,tmp2=B;
	if((S+A+B)%2||(S+A-B)%2){
		cout<<"No\n";return 0;
	}
	A=(S+tmp1+tmp2)/2;B=(S+tmp1-tmp2)/2;
	if(A<0||B<0){
		cout<<"No\n";return 0;
	}
	solve(A,0);solve(B,1);
	print();
	return 0;
}

Part3：背包的优化

优化1：(max,+)卷积的引入

好像实际运用中不一定能优化，但这个卷积挺重要的。

考虑多重背包问题，但是 $S$ （背包容量）不太大，一个显然的做法是对 $w_i$ 分类，有 $O(S)$ 种，每一种就枚举选了多少个，这样暴力做实际上是调和级数，就可以做到 $O(S^2\ln S)$，用了二进制分组还会更快，但我们要讨论一种 $O(nS)$ 的做法，当 $n\leq S$ 的时候往往表现更加优秀。

记 ${\rm dp}(i,j)$ 为只用前 $i$ 种物品，总重量为 $j$。

转移为 ${\rm dp}(i,j)=\max\limits_{0\leq k\leq K_i}({\rm dp}(i-1,j-k·w_i)+k·v_i)$，如果对相同的 $j\bmod w_i$ 单独做，可以用单调队列优化，这里我们不讨论，来讨论一个推广性更强的优化。

(max,+) convolution

题目描述是这样的，有两个长度为 $n$ 的序列 $A$ 和 $B$，通过卷积得到 $C$，卷积形式为 $C_i=\max\limits_{j+k=i}\{A_j+B_k\}$。

$O(n^2)$ 的做法很简单，但已知的最好做法是非常惊人的 $O(\frac {n^2} {\log n})$ 或者 $O(\frac{n^2 (\log \log n)^3}{(\log n)^2})$，而且很不好写，不适合算法竞赛。

但在一些特殊的性质下会有更厉害的做法。

(max,+) 卷积和 (min,+) 卷积本质是一样的，由于 (min,+) 比较常见，就讨论这个吧。

先从最特殊的情形入手，$A$ 和 $B$ 都是凸的(斜率单调)(对于max+卷积要是单调减小，对于min+卷积要是单调增大)

这里的单调是非严格单调。

可以直接把两个函数图像画出来，然后贪心地去合并，具体来说是从 $A$ 和 $B$ 中选择斜率更小的那个走，可以理解为 $C_i$ 要从 $C_0$ 开始走 $i$ 步，从 $A$ 和 $B$ 的前缀斜率中选择共 $i$ 个求和，由于都是单调的，贪心选小的肯定更优。

这个过程是 $O(n)$ 的，更为正式的名称叫做闵可夫斯基和。贴一张CF原博客上的图。

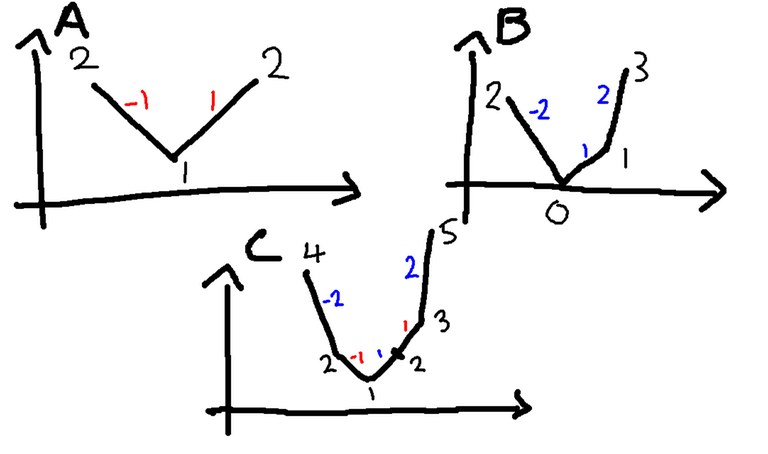
这个最特殊的情况已经可以解决一些单调队列优化或者斜率优化的题目了。

接下来考虑不那么特殊的情况，只有 $B$ 是凸的。

先给出一个 $O(n\log n)$ 的做法。

定义 $i$-chain 为 $A_i$ 与 $B$ 中每个数卷积形成的一个函数，第 $j$ 个元素为 $(i+j,A_i+B_j)$ 。

其实是把 $B$ 进行了一个平移，所以是凸的，结论是任意两条 chain 只会有最多一个交点。

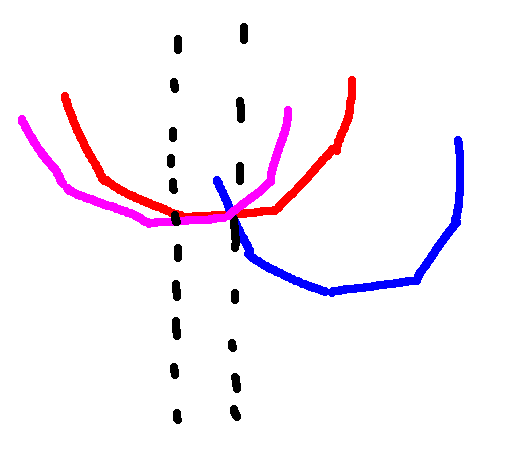
接下来我们来证明这个结论。

记 $i$-chain 的函数为 $f_i(x)$，那么有 $f_i(x)=A_i+B_{x-i}$，我们想要 $g$ 是非严格单调递增函数，即证明当 $i<j$ 时，存在 $k$ 使得 $g(x)=f_i(x)-f_j(x)$ 在 $x<k$ 时 $g(x)<0$，在 $x\geq k$ 时 $g(x)\geq 0$。( $i,j,k,x$ 均为整数)

$g(x)=(A_i+B_{x-i})-(A_j+B_{x-j})=(B_{x-i}-B_{x-j})+(A_i-A_j)$

所以 $g(x+1)-g(x)=(B_{x+1-i}-B_{x-i})-(B_{x+1-j}-B_{x-j})$，由于 $B$ 是凸的，$i<j$，所以 $x-i>x-j$，所以 $(B_{x+1-i}-B_{x-i})\geq (B_{x+1-j}-B_{x-j})$，所以 $g(x+1)-g(x)\geq 0$。

有了这个结论之后，我们就可以把 chain 以函数的形式放在李超树上，维护出凸包，复杂度是 $O(n\log n)$。

但运用 SMAWK 算法可以做到 $O(n)$。这个太难了，不讲。

SMAWK 贴个链接：

http://web.cs.unlv.edu/larmore/Courses/CSC477/monge.pdf

用完 SMAWK 的后续步骤原博客也有提及，这里不再写了。

优化2：(max,+)卷积的应用

这种优化适用于的特殊情形：

有 $n$ 个物品，第 $i$ 个重量是 $w_i$，价值是 $v_i$，找到一个集合 $S$，使得 $\sum\limits_{i\in S}w_i\leq C$，并且使得 $\sum\limits_{i\in S}v_i$ 最大化。

其中不同的 $w_i$ 只有 $D$ 种，这样的限制下，利用上面的卷积我们能得到一个 $O(DC)$ 的做法。

单调队列优化是 $O(nC)$ 的，做不了，但根据决策单调性可以做到 $O(DC\log C)$。

首先从 $D=1$ 开始，很容易想到贪心，把 $v_i$ 降序排序，然后找到最大的 $k$ 满足 $kw\leq C$，答案为 $\sum\limits_{i=1}^k v_i$。

然后进行拓展，对于每个 $w_i$，把 $A$ 按照对 $w_i$ 取模的余数分类， $B=[0,v_1,v_1+v_2,...]$ 这样一个前缀和数组进行 (max,+)卷积，由于 $v_1\geq v_2 \geq v_3...\geq v_k$。前缀和的斜率为 $v_i$，为下降的，满足 (max,+)卷积的条件。每个 $w_i$ 要进行 $O(w_i)$ 次卷积，每次卷积复杂度为 $(\frac C {w_i})$，所以是 $O(C)$。

例题：NAIPC16 thief

就是上面的板子，但是由于我既不会写李超树又不会写 SMAWK，所以不放代码了。

优化3：通过重量限制略去多余转移

有 $n$ 种物品，每种的重量为 $w_i\leq D$，找一个可重集 $S$ 使得 $\sum\limits_{i\in S}w_i\leq C$， $\sum\limits_{i\in S}v_i$ 最大化。

我们可以在 $O(D^2\log C)$ 的复杂度内解决。

定义 $ans_i$ 为重量为 $i$ 的最好答案。容易观察到 $ans_i=\max\limits_{j+k=i}\{ans_j+ans_k\}$。

显然可以在 $|j-k|\leq D$ 的时候取到最优。如果差大于 $D$，就从大的里面拿出一些物品放进小的里面，由于 $w_i\leq D$，所以肯定可以让绝对值 $\leq D$。

基于这个，有很多种实现的方式，比如初始暴力求出 $[ans_0,ans_{2D}]$，然后通过卷积不断保留长度为 $D$ 的区间，直到这个区间包含了 $C$，比如 $[ans_{T-D},ans_{T}]$ 和 $[ans_0,ans_{2D}]$ 卷积可以得到 $[ans_{T+1},ans_{T+D}]$。

这个每一步操作都是一样的，所以可以倍增做。

或者要求 $ans_C$，那我们先求 $[ans_{\lfloor\frac {C-D} 2\rfloor},ans_{\lceil\frac {C+D} 2\rceil}]$，然后求这个继续拆解，两边向外拓展的界，得到要求的是$[ans_{\lfloor\frac {C-3D} 4\rfloor},ans_{\lceil\frac {C+3D} 4\rceil}]$，这个序列长度无论如何都不会超过 $2D$，所以就暴力做即可。

注意，这个优化中所有卷积的序列都不是凸的，暴力就好了。

总复杂度为 $O(D^2\log C)$。

例题：USP16 knapsack

这就是上述的板子。贴个代码。

#include<bits/stdc++.h>
#define forn(i,a,b)for(int i=(a),_b=(b);i<=_b;i++)
#define fore(i,b,a)for(int i=(b),_a=(a);i>=_a;i--)
#define rep(i,n)for(int i=0,_n=n;i<n;i++)
#define ll long long
#define pii pair<int,int>
#define m_p make_pair
#define pb push_back
#define fi first
#define se second
#define int ll
#define foreach(i,c) for(__typeof(c.begin())i=(c.begin());i!=(c).end();i++)
using namespace std;
const int N=1050;
int n,C,D;
int dp[N*2];
int f[N*2];
int g[N*2];
void upd(int &x,int y){
	if(y>x)x=y;
}
void dfs(int l,int r){
	if(l==0){
		forn(i,0,r)g[i]=dp[i];
		return;
	}
	int nl=max((l-D)/2-3,0ll),nr=nl+2*D;
	dfs(nl,nr);
	forn(i,0,r-l+1)f[i]=0;
	forn(i,nl,nr){
		forn(j,i,nr){
			if(i+j>=l&&i+j<=r){
				upd(f[i+j-l],g[i-nl]+g[j-nl]);
			}
		}
	}
	forn(i,0,r-l+1)g[i]=f[i];
}
signed main(){
    cin.tie(0);cout.tie(0);
	ios::sync_with_stdio(0);
	cin>>n>>C;
	D=1005;
	forn(i,1,n){
		int w,c;cin>>w>>c;
		upd(dp[w],c);
	}
	forn(i,1,D*2)upd(dp[i],dp[i-1]);
	forn(i,0,D*2){
		forn(j,i,D*2){
			if(i+j<=2*D){
				upd(dp[i+j],dp[i]+dp[j]);
			}
		}
	}
	if(C<=D){
		cout<<dp[C]<<"\n";return 0;
	}
	dfs(C,C+2*D);
	cout<<f[0]<<"\n";
	return 0;
}